orpheus
記事内に商品プロモーションを含む場合があります
放物線の性質1
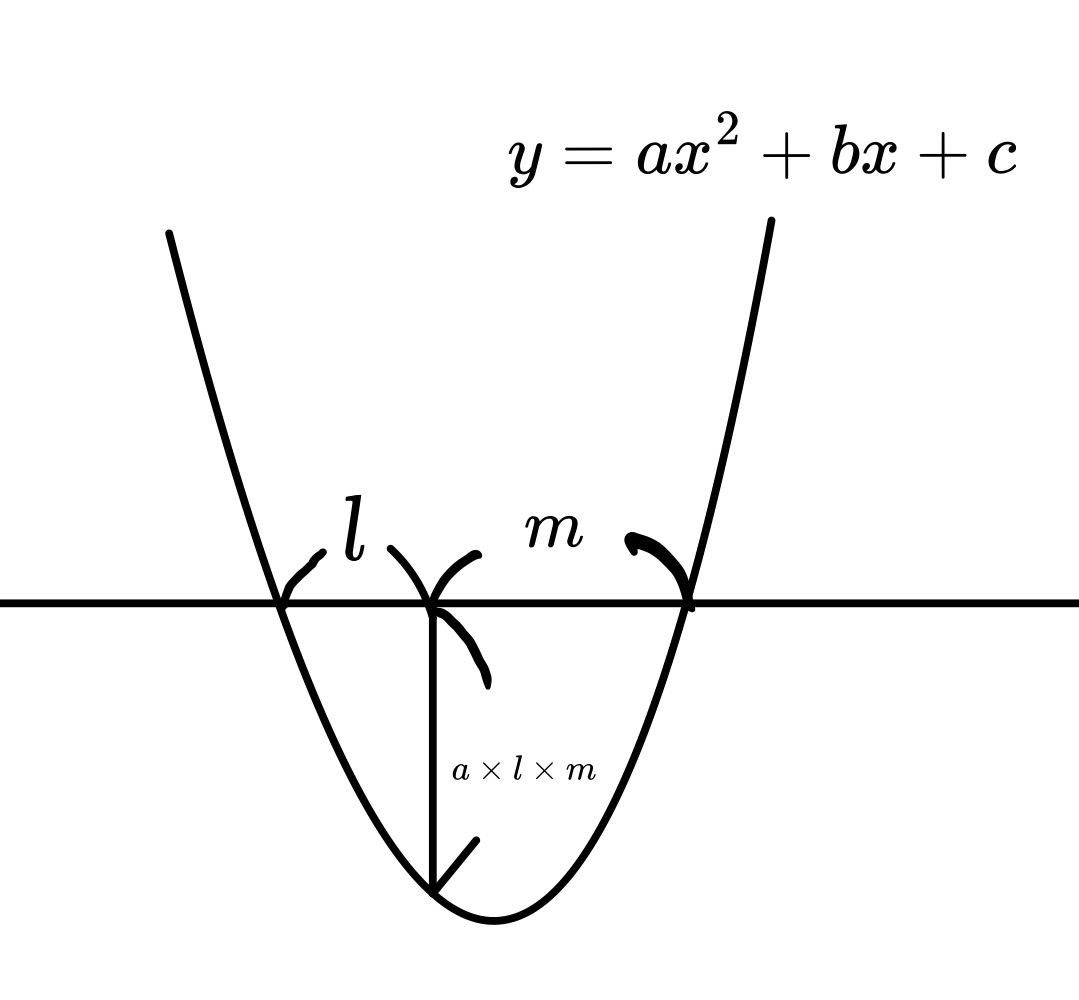
\( y = ax^2 + bx + c \)
と
\( x軸上の点から下ろした垂線の長さは \)
放物線までの距離のかけ算で計算出来ます
\(垂線を下ろすx座標をtとし切片をx_1,x_2とすると\)
\( 切片がx_1,x_2なので放物線の式はy=a(x-x_1)(x-x_2) \)
となり \( tを代入した式 y=a(t-x_1)(t-x_2)=a\times l \times (-m) \) で
計算される\( y 座標がマイナスなので結局a \times l \times m \)となります
関連
ABOUT ME
公立高等学校で数学と情報科学を教える教師です。
授業では、iPadを活用した指導方法や、数学の新しい解法を生徒たちに紹介しています。
音楽にも深い興味を持っており、特にピタゴラス音階や純正律など、数学から派生した音楽理論に魅了されています。また、合唱のアカペラでのハーモニー作りにも情熱を注いでいます。プライベートでは、コーヒーを楽しみながら様々な音楽を聴くことが趣味です。このブログでは、iPadの便利な使い方や数学の面白い解き方、音楽理論についても掘り下げていきたいと考えています。