放物線その2
orpheus
記事内に商品プロモーションを含む場合があります
面積その1
簡単な計算
上側の直線の式ー下側の放物線の式
＝上に凸の放物線の式
で求める面積は
上に凸の放物線 と \(x軸\)
で囲まれた部分の面積になります 放物線と直線で囲まれた面積は下の図で
\(直線の式-放物線の式=上に凸の放物線\)
で \(x軸\)と囲まれた面積なので
\(\dfrac{1}{6}(切り取られる弦の長さ)^3\) 弦の長さは\(x軸\)と平行
で計算することができる この事について色々な場面での計算とその理由を解説していきたいと思います
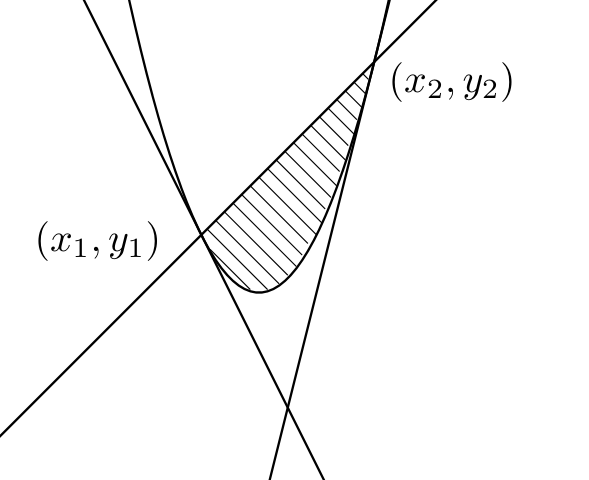
結果だけ先に示しておくと
放物線の\(x^2の係数a=1のとき\)
上の斜線部分の面積は \(\dfrac{1}{6}(x_2-x_1)^3\)
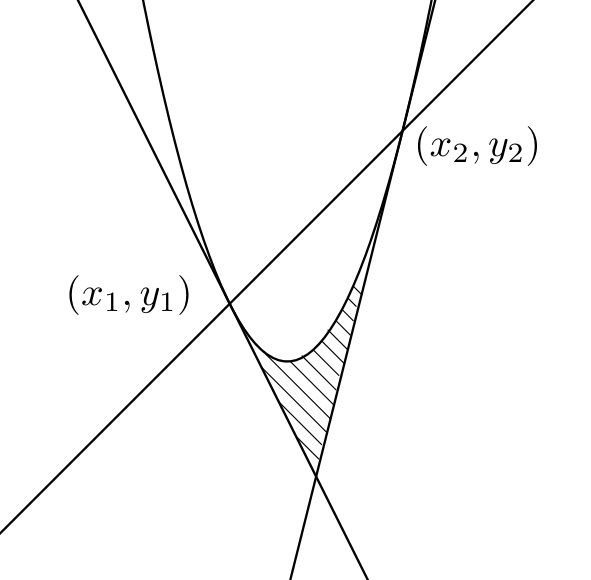
下の斜線部分の面積は \(\dfrac{1}{12}(x_2-x_1)^3\)
上の斜線部分の面積は \(\dfrac{1}{6}(x_2-x_1)^3\)
下の斜線部分の面積は \(\dfrac{1}{12}(x_2-x_1)^3\)
ABOUT ME
公立高等学校で数学と情報科学を教える教師です。
授業では、iPadを活用した指導方法や、数学の新しい解法を生徒たちに紹介しています。
音楽にも深い興味を持っており、特にピタゴラス音階や純正律など、数学から派生した音楽理論に魅了されています。また、合唱のアカペラでのハーモニー作りにも情熱を注いでいます。プライベートでは、コーヒーを楽しみながら様々な音楽を聴くことが趣味です。このブログでは、iPadの便利な使い方や数学の面白い解き方、音楽理論についても掘り下げていきたいと考えています。
授業では、iPadを活用した指導方法や、数学の新しい解法を生徒たちに紹介しています。
音楽にも深い興味を持っており、特にピタゴラス音階や純正律など、数学から派生した音楽理論に魅了されています。また、合唱のアカペラでのハーモニー作りにも情熱を注いでいます。プライベートでは、コーヒーを楽しみながら様々な音楽を聴くことが趣味です。このブログでは、iPadの便利な使い方や数学の面白い解き方、音楽理論についても掘り下げていきたいと考えています。